Sixteen Ways of Looking at a Fractal

(Literary readers: yes, this is a reference to the Wallace Stevens poem, “Thirteen Ways of Looking at a Blackbird.”)

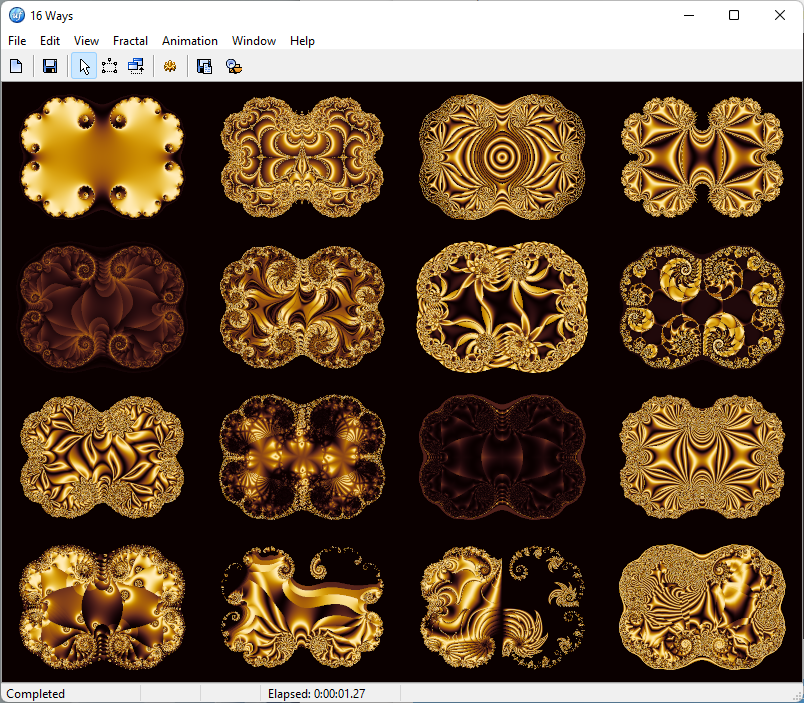
This image has 16 fractals arranged in a 4 by 4 array. All 16 have the same gradient and the same Formula tab (Julia from Standard.ufm). All of the Outside tabs use Plug-in Coloring (Gradient) from Standard.ucl, and the Distance Coloring plug-in from jlb.ulb. The differences come from the options in Distance Coloring and to a lesser degree in the gradient’s Color Density, Transfer Function, and Rotation.

For the top row, all four fractals have both horizontal and vertical symmetries. Fractals in the next two rows have only symmetry under a 180-degree rotation. Fractals in the bottom row have only the symmetry of the outside boundary.

alt="61d34c9227185.jpg">
16Ways {
::X3D5Bin2t31WzNqRW43nqm/DU6pxbikhGadZ2iHyMZykbzmUZms7LbtqQQLLSQAGQ+WN/43m
GEyW0nGw2SWW+8SyY1nTfjTf57crnn44m5E82X/KNtM/sAmdPjha/HnrT7pdpvX2C7x66aLY
+ntIzeI/fG4cNLJ12YUOHuJMP/sU7e/s/St3Fsi9PNO18UiOh0TzJMz3Jw3J1P8M7rZpv+VC
WFtkrTcmfUodvPvMKKbRPtoYHX/srtN4twSWyZslReM7g8WlFy/lsFRe2LXFk5H7kmK6sJOh
pxOJswsiafpTcMvpKqf+vySs1PlXbOnFarPwcEl3jOjP+moXw78okl8xxrfV1fJYdufAL0ZJ
fe4zZOheOJeDWd18ea8aM5a7efkFyS8d/yae6lzT80q649B8+ndv/KY2gVBze7P/rvb6niug
9eRHSKxDuY6ZFVqY0Lp4qfInAgqYVKL5O0VnoFRJ+3wnKMIU5VCvGWXc+vuKwRMjs05K/8ZT
TTLtYWi7Cm7fbHNfumj3ftKVM7LdWbexkT5E3PviLL0j3qpMmX+HkTz7ixRXyrZi4fPzxPIa
VWxg0PM13j92qv0z5kFGFy0SjC89stIjpWDtojG+6Xx5pOtB+hMnkSq1l2/cDud/r8D7HTc8
85/07jC4TXhnV+Jzt8Pl85979T5VpLTFH1+Gvdpr/7NfhrxfZH72UWjsihrY5Q964Gvbsvp2
vWsooeVNnT8NiFEbVwPYzXRvoe9Ybcq0u+8/8LbvegNzfV6fylY3eZUNOv7EHMRSWiIjsarS
gJVWv0mAzBf+6iazViCynvg4yRXsJl0iMUMjOwhkXq0imprixZG29B5kAxZ2lRec5c+Sw6yc
VSkfKyTGvh8BStfUUb3dd0n9XGHwISFFyJvZZhSqWvi0mYYobMBmS+BZ5nCRM0nQskTj4cIg
BmbHHEutbU42+hhbbGHuNOQq+ESypo+HQS+xkynEJbN+fvfibALF8jIpdfFJ1H/A0Fuapie3
g0FOx8aAo0FRXa/bJ+n5H6EAXHxRBOJyE9LKOxwmAzsnbGnAZLyL52xTJ/89nNsBZW1XGRTT
KPcFopJN00E+d+g42sp220uvyG3shGn3AEQ2taq1t4T6E4G3qhG3ivNJcrTbq1p8Wvvimn2Q
zTt7DOz7HON/eS/k4KSqEbvUyGvpRLZTdCCs7p9Z+/U6CV+6O+VBHW735LXW6EeN0CXBbEJt
ZJfACrXmdNfJqklXxXmffUq0RYOWAbvaH4+R5XOZG05aui2u3v6kmpte/me1HY/tf8UnLOj3
JlexqmOBce++L29+E/mnsgZJRZa5Nb92p82wyqibd54allwc9jF9t1XSUcX4UB2Kx1z5NpjA
w1EqmPvTcltFlqJqFeNW+TUCZ9PN2akh1w8KpsoxjXX0whmWWl/MZTlYMhQMGtu2NJiBhEWM
3UTrbkSsf3uPzFGKIXvCZIvtkigs4AntRQeX8i7MwiqgXccBakPlggGfpCas/NTjTYXAhdU6
We5wHRsjI2x9D2xyTBeCgOaYABdUc1iiOGY9EbPgKvkU3EGLca5hTArOFUerzvkWeC8dVL3e
nAOIzgvmKomjEF2q7oCcFVRReRTTddCYA35CxejYvRs3I27jUs30XOYv/RnklRh+uafHfvUn
zegwvBwe/v4oAkxbJUCY42fgItvXA5Wcq8LWM3av5DBB+xpsTUj+GtW7DB49wjYr16x48xla
MBggTGpPkaZiAxXDE/0Y/rYBPR4w3M3zn7W/HT/F+d099i4XjNmdohEP96lRJecpKLFUkwmH
wczsL//+XwUQsCsW5UUU8S+WIQfGF4vFfuM1VgUWJSB5AFMgvW0BFYZQyEXHo8IFI0ywoRfM
xLTaAv8odGe5frY3xHEgZgxOiYGRMjImREzIi5n7ImXvVjWSOAzDL8y6PY4yWk1wl1JbDX2a
4EQ4ymUpwl3UJ3FuMZ4EI4ybqpdpJqRnceXCbe8LC7VHdGas626hzW0OhP+8EZk7YPgeq+AC
FElcCrYi7P+w7m6kllHeFTLF0mmd1hntqL7jRboXsNMfTDdCo9qLGP2/qTWUkrTycfHQrUL2
jranEpkwXmlyyy3IDE5NTANnvZK0BTboa6Mus+vL0Ti3aP6CijsFJs0FRBe2GDkjo3PMHvya
rQK1G9ck38VmhZAlSKKFqL46wv6GFo1dnxLcyAw5FXXwO+SnclHOCizF5FbJvoZ5VKIjucGl
3kLIiKFkTyMwe7Cir8rbJmDvyWOXzv2GsfG7YTGYKfEGPLvfaCyqrdf+cHVeheccCKY+cHbT
LgR55KnZP31GSOIjLkQpwsmlLnAxLf0YRg5NwBm3gZ8JxJgcmLKMWeR5n+BK8dTuciJdk0VM
x5LoKd7FgyJ2uRpQFa2AzWqYmqi5gyeGUhkGY2UFzWqc1n4AnQm9V9vW+eUZiIyDepQBBE5f
pK5GcTVhOl4L5NkvNTV5grIWsmEKwS/qyBHAFUAJleez9hsKS0NlPN0Yn4G1DjiDfg3PK98i
JaAuPf9QEs9Tz4wAOjj8QWP4Fhmj39uZl8pvHJtGv78yqP4ntglgKNGVaMq0YUpxoSjfeFiT
9fi8zKpjv1qOOXfX3z4cKHi+jboN1OFH3nYVp5Yz7qB3NqPGQnvGmDBUT8mqSQ/GFOT2WX0V
qPuqq0foaO+znvyJhp9m/gf1SxFBOpBtILUl5+K6nexnqMEBF1zetIneO6vVY2yAj4pnZZLD
xRDHmOxV1xVAYu5bB1IaZZLY3gX24RwPw8aCSfxidCB46ZdwttKPS+9RJ8L0kx8gxpv5IHMm
oQw6IYdEsOCW/lnHe9yJfkUBNnOsesRZCHbUTkHbUDhiNKTwYjayjrze9xEfvKA7cchJnYgh
H1TWeJBEhOlq/sJ8oMGYSxIka/hYvwbeqDZXP33vQQ7H9g2VbC9efyPkv/uTw3+T8tjPp3Dx
e65HW8oChXfEZcbgwrbQaFE+8Dw2HQtPLJfzsTNgHmJCSMgsjfxycrWhdGkg47H66HZw1QfD
P4RFn3xRUxIqYEV8zBTYrDDL2Sv7Gxur4idcjSXIFZp0T9rH6ThNZCbJ90nMLY3KwwmTqsT9
QpmWmaCliPMmMBKMnGCY/aTTic7Xvpqew2v+TCQuBs3qVGX3frWrCGK0M27zcIyRBIZCiQ+h
hQGI6o69Dvx5fczNccO1BKHEdm8gky40BjoISZ0823bzbv+kjnEDcrTAcX6cYMqMc9l2fX41
wQQ5/HjO6R9Cea5YdNttdEXSf7MsfBxtxZ7LoUVuapgiOo+AB9NpDhCqUltTLoQp34XNnk1Y
/Xx+m3iqW6hAlTa5gBagmGcCgKKJ3DJNSHk0IdUSj0FJNSrl0INKpR6okGpVSac8h2mNUPNK
pRajkGpVSatEw5tRd2ANtVQzsjemkgnOIoZ2RBNzuIoZWIoV0nbgyC/WSFFlfwbu7l1IRdTm
182qYtBKbj0kZHkmMX7eTNpjuSqbW2zsx4SqiUr7hwnVHE+s6ownVXE+satwnVjCfWtS4zqN
CfWdU4zq1CfWtS4zqDCfWdS4zqFCfWtX4jePE+odQ4j2RhPaXE+otW4j2owHtVCf02I8R7ow
Ht1Cf0WJ8R7gwHtTCf0WI8RxIyEdyT0cWo5sQn8ET89HsJyvXoWzSrUV4arPv9AyIWvceJ6G
P6FQMZuJz+h2va3Z/KMJ/hJ5PMJ/hJ5PMJ/hJ5PMJ/hJ5PMJ/1k2E3xeeRuqEhDi+8LZ0LPo
L+f5hfRPU7oo2RRtjiaHFd2/jy8V3Wu6/R2rcywxr1OKZctX5kJUwAffoh0AffTlslCTnQhC
89N10jTgvvxX/LOwZtr+rZr5EGuKYV6d0XK6i/7zMV3wjj37E0x+xkVH6N/o38v38m/gA0b+
L8mfL0b+Rv5fv4N/Wdyb+baer1OzPZv6M/9Noo78juz/hs78XltSR/5H9n/9u/83OpP0h+RH
6fX4Q/tT6D9o/drNr2BmsSBptal2duKLkW+VZIhWvYoxbuq8SrqvvaTXVlo8ZH7BaujtuOKw
Uw2GFByiIy49WGFB0iIK4Tm9SWbREpmLoI/HZAZREZqa7eaUkvLxPbBfPqj4nxnjPLj8lLje
rW98C8JfTxv9752y+EJGHppXIe0cJ7q0G8zazlUlRkGM6WpNY3VzYolT6klT6PsLmOhPel5J
5GnOAzESH72OB6OMdKpBb9Ul0gbrhUI6HgJNYrTNbKnBrKjBbq3cGDW2loexlygVK1tjxjpQ
wrEPWPNxto69og7yrRgXFyVKSX1kSZPqa4VK6DNrteytk/kJi+k6WZkunCZNY9J7jcI7/2Jx
XA1Qz8ILByeECd6NHoxb7L+kG7RiHlVFnt6Ico7bE2KWk2DwbygSQs6Yw1iBXLGctYw1iBXL
GctYw1iBXLGctP9BX7XzVR5X/mvmrkyviBYLGgtYA2iBYLGgtYA2+8LAbnQreZpp1fZpJwvs
0jl/ySTheZpJgvs0jfc1FapPn9mynSrTwnV6nskM4Rh/hYuhr0zxoqFQZo9vZacC7iOqT0bu
BDuW0BR2PBXbThC4O0jQUFSCiLZUeWlcKU9w90e3EpJvEJRZM+qIm+E71PCk3iNAAuwaLj5A
YHkuJHAAxhj4wRc4IOc8ZA45+zAwG3Ry4I7FAYywKI4DrDB3EGC+E5QwHCBB3EEC+kHXI4VP
AAx+JOBIA8ns8Z14RHBAwvT8ZgeikMw3xCvQRO2bL69Il/zH8Auk0ACiDHxh/AwhXeoweDHu
46Di9maPKaAI0ZqD2eHIQqxg3RKv0ZI2WEbLitFx2iYbP4sx8+Bb7HZ8piskD5sVwHIPs0VQ
fzR1R5enHzu7AP9uQXN448UD1dbwxmbwNrX9E3p/4iytMrHpOabQ8u7zESAIeXKV/ZUCJYyw
hDHpOfOD95mj/FB/ePN8MmaCeJj49hnZCatzN3Q6yb3aJaFokbIn4pKb41UewrIRatzz1BFr
6Vk0YbnBn3O92pws0NnXEO+T6B7GU35dcE1Ni6GRd/cA1tOMsbrunkL63Vc33vccxW+29xVa
u447ll/LJ+iD4VbRZEe9uKZWcUAv2Efok23ArvHe09m5e+c36/Y6vwvPtvXE/qrxsDNk1pXv
MKxjLVZpgiE2cR07W+/9vgpgYFgdE5kBRxL5bhA9ZUgnuM/t9UFJv89sPsQ6ehhSj4eB/2vQ
oLvwkzqZDu6saPd+D+ZLUYJ62D8UhBlR7Gj2NGRwiIYREsH52N+Hd4H/HeLzGfc5Y0HfAY/N
+3p/kTby6X/3Nhp83qxBOGjv9vPZBr8xG4W2VxonS3JMt9JkBU0gxoBjP0MYc1xGPR5DrJA+
Ddifmtp6clFA0tq39r8h294NbNntO8gyVSeXeT5KYp9PrcC6vdwc3M1xN8kwJIqbvKcCWa57
Cng2E7WMsKOBtdzXZN8QvJorNPIdCC7wDJcxUajP0cCya9LdIfVXSNFaxvmWjM1BhzSy7iwp
glCdEAop08e5nzJ4/mXRvPJKNtXbqvu2vXzE/sk4iOEvzj+7A6vDo2iQtFh+7wBm/Oc8+mew
xutWZR6Up6xh/vhUWkJ0L4xmqaLlFRGZIXZRbqqHsyieXgj7frJKo7BZAqVoHnIo3AKF2Z8A
0Jk4RDo3jwzyRh/L0QcA89s5OcBjetYV04KNuadPV65/HYh68GG=
}

Here’s a simplified description of how UltraFractal makes images.

For each point (#pixel) in the plane, an initial Z is defined, most often either Z = #pixel or Z = (0,0), the “origin,” the point x=0, y=0. New Z values are generated using mathematical formulas as defined on the Formula tab. Think of these successive values of Z as marking out a path in the plane. The iterations end when the bailout criterion has been reached or when the limit on the number of iterations is reached.

The Outside tab (and sometimes the Inside tab, too) calculates a color to be assigned to each point in the plane. For Gradient-type coloring, the formula calculates a number for each point; the number is used as an index into the gradient to determine the color.

Some plug-ins use only the final Z value at each point, such as the distance of Z from the origin.

The Distance Coloring plug-in has (too) many options.

First is the Accumulation Phase where information is saved about each iteration. Information can be accumulated based on Z or various manipulations of Z, called ZZ. This phase uses plug-ins to calculate “distances,” either real or complex numbers. There are many plug-ins in jlb.ulb, each with parameters.

Distances can be accumulate using all the iterations, or just some. Each of the 16 fractals uses only iterations from the sixth onward.

In the Final Phase this accumulated information is converted to an index into the gradient, with (too) many options.

Experiment. To work on any single fractal, delete the mapping (which just moves the center), change the Solid Color from transparent to Black, and change the magnification from 0.375 to 1.5 by pressing F9 or I twice.

I can answer any questions posed in the replies.

I thought I would take a peek at your parameters but I'm afraid there is a problem with them; UF is reporting over 90 errors when I try to open the above parameters and many of your example images are not being reproduced as you intended.

The errors mostly say things like:
!Could not locate parameter 'fut' in 'GenericGradientColoring' in Standard.ucl
!Could not locate parameter 'center' in 'GenericGradientColoring' in Standard.ucl

When the image finally opens this is what is displayed:

There is something very wrong here, any ideas? I have updated my formulas but no joy.

I apologize: I had forgotten to update my formulas after doing a lot of cleaning up. I just updated them, so please try again.

Yes, that's fixed it. Thanks!