Hello!
I have been lurking here for quite a while, with only the occasional post, but over the years I have spent lots of hours in UF, and I enjoy it a lot. What got me into UF originally, was the fact that I can write my own formulas, which I have repeatedly done.
Just last week I tried a way of combining the Mandelbrot Set (nice shapes, but nothing new at this point) and the Burning Ship (interesting, but often rather difficult to color, and sometimes flat out noisy and nothing more).
Here's what I did (published in phs.ufr).
init:
z =
y =
int k = 0
nb = 0
loop:
z = z^@exp +
if nb < @nbmax
y = abs(y)^@exp +
nb = nb + 1
endif
k = k + 1
if k == @n
z = @t*z + (1-@t)*y
k = 0
nb = 0
endif
Basically, the fractal calculates a Mandelbrot and Burning Ship at the same time, and every n iteration, it replaces the Mandelbrot z with a weighted mean of the two fractals. In this example, the coupling is one-way, the Burning Ship is never affected by the Mandelbrot values.
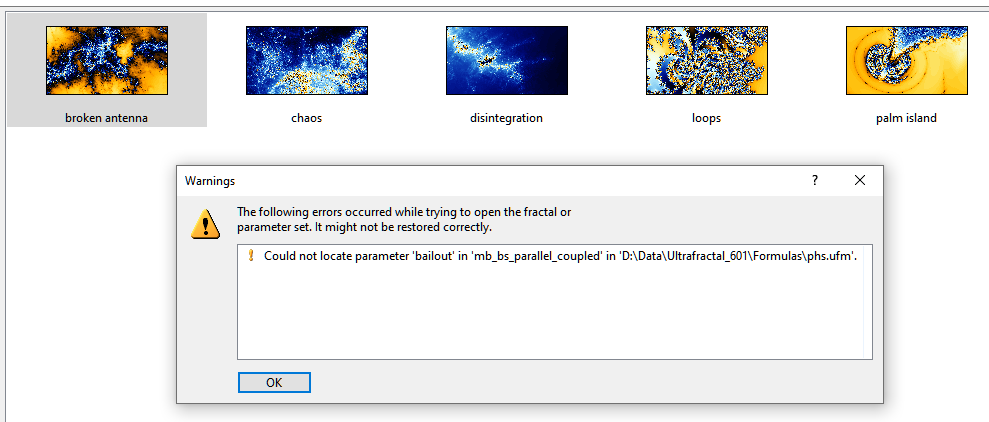
I have just uploaded phs.upr with five examples of what the formula can do. Here are the examples:





Hello!
I have been lurking here for quite a while, with only the occasional post, but over the years I have spent lots of hours in UF, and I enjoy it a lot. What got me into UF originally, was the fact that I can write my own formulas, which I have repeatedly done.
Just last week I tried a way of combining the Mandelbrot Set (nice shapes, but nothing new at this point) and the Burning Ship (interesting, but often rather difficult to color, and sometimes flat out noisy and nothing more).
Here's what I did (published in phs.ufr).
````
init:
z = #pixel
y = #pixel
int k = 0
nb = 0
loop:
z = z^@exp + #pixel
if nb < @nbmax
y = abs(y)^@exp + #pixel
nb = nb + 1
endif
k = k + 1
if k == @n
z = @t*z + (1-@t)*y
k = 0
nb = 0
endif
````
Basically, the fractal calculates a Mandelbrot and Burning Ship at the same time, and every n iteration, it replaces the Mandelbrot z with a weighted mean of the two fractals. In this example, the coupling is one-way, the Burning Ship is never affected by the Mandelbrot values.
I have just uploaded phs.upr with five examples of what the formula can do. Here are the examples: